The Science Behind Beam Properties In The Civil Engineering
Beam Properties In Civil Engineering |The Science Behind Beam Properties

The Science Behind Beam Properties In Civil Engineering
A beam is a fundamental structural element that primarily resists loads applied laterally to its axis. The deflection mode of a beam under load is predominantly through bending. The Science Behind Beam Properties In Civil Engineering
Understanding Cross-Sectional Area, Torsion Constant, And More
A beam is a fundamental structural element that primarily resists loads applied laterally to its axis. The deflection mode of a beam under load is predominantly through bending. It’s crucial to understand that the behavior of beams under load involves a combination of shear forces and bending moments, inducing internal stresses, strains, and deflections. Beams are characterized by various factors including their support type, cross-sectional profile, material, length, and equilibrium conditions. Historically, beams have been made from materials like wood, metal, and stone, and are used to carry both vertical gravitational forces and horizontal loads, such as those from earthquakes or wind.
Influence of Cross-Sectional Area and Geometry
The cross-sectional area and geometry significantly influence a beam’s behavior under load. The cross-section determines the distribution and magnitude of internal stresses within the beam for a given load. Various cross-sectional shapes like rectangles, I-beams, and H-beams are chosen based on their effectiveness in different structural scenarios. For instance, I or H sections are typically used in steel construction for their efficiency in resisting bending due to the distribution of material away from the neutral axis, thereby increasing the second moment of area.
Material Properties and Beam Strength
Material composition significantly impacts beam strength and the way that beam dimensions are calculated. While geometry determines the stress distribution within a beam, material properties such as yield strength, tensile strength, and modulus of elasticity define how much stress the material can withstand before failing. For instance, steel beams can support greater loads and span larger distances than wooden beams due to steel’s higher tensile strength. Advanced composite materials are also being used to enhance beam performance by combining materials like carbon fiber with traditional substrates to increase strength-to-weight ratios without compromising on structural integrity.

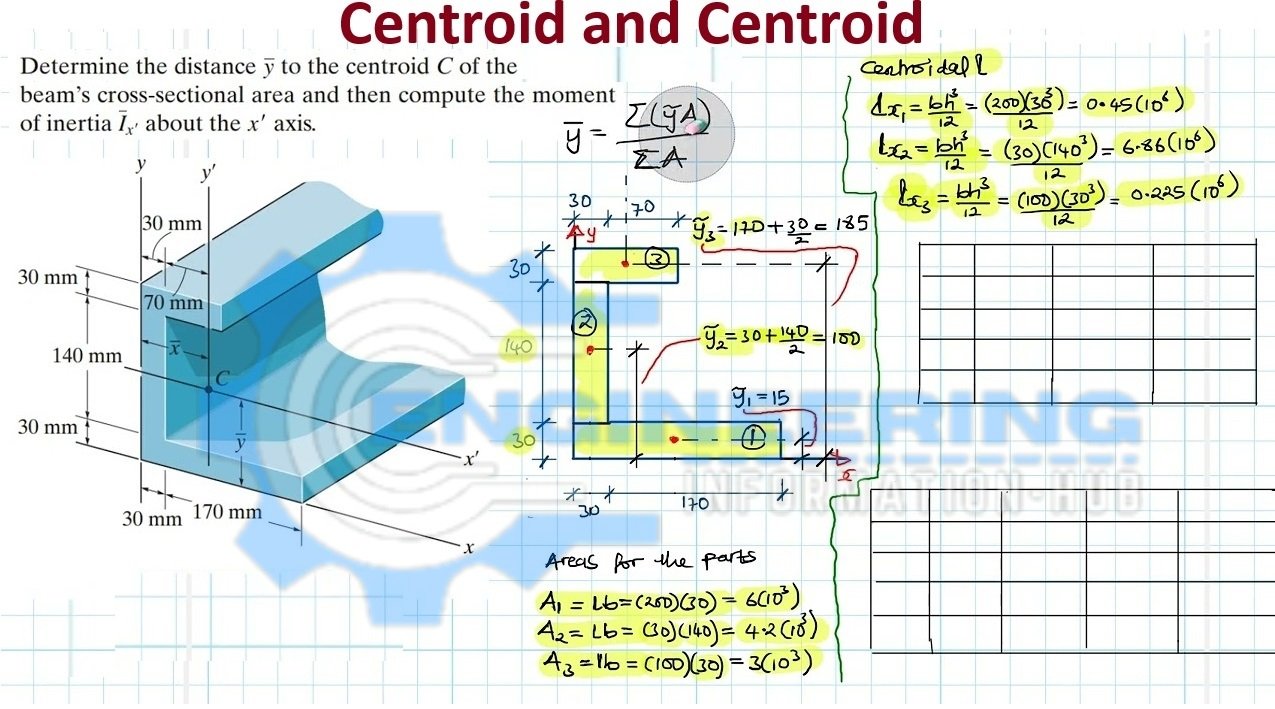
Centroid and Centroidal Distance
The centroid of a beam’s cross-section is a critical geometric property, representing the point about which the section’s area is evenly distributed. If a cross-section is symmetric about one or two axes, the centroid’s position can be easily determined. The centroidal distance is the distance from the centroid to the extreme fiber of the cross-section, influencing the bending stress distribution.
First Moment of Area and Its Significance
The first moment of area is a measure indicating the distribution of a cross section’s area relative to an axis. It plays a pivotal role in determining the shear stress distribution within the beam, especially under transverse loading conditions.
Area Moment of Inertia and Beam Bending
A crucial aspect of beam analysis is understanding the area moment of inertia, often referred to as the second moment of area. This property indicates the beam’s resistance to bending and is calculated based on the distribution of the cross section’s area relative to an axis, typically the centroidal axis. The moment of inertia is integral in predicting how much a beam will deflect under a given load.

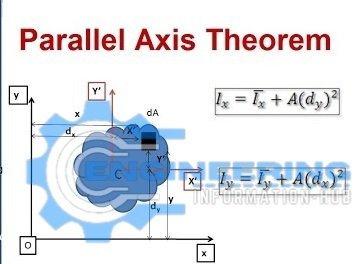
Parallel Axis Theorem in Cross-Sectional Analysis
When dealing with composite cross-sections or those not aligned with centroidal axes, the parallel axis theorem becomes essential. It allows for the calculation of the moment of inertia about any parallel axis, given the moment of inertia about a centroidal axis and the cross-sectional area.
Understanding Torsion in Beams
The torsion constant is a geometric property of the cross-section that plays a vital role in the beam’s resistance to twisting or torsional loads. The torsional stiffness of a beam depends on the cross-sectional shape, material properties, and length. In beams with non-circular cross sections, warping deformations significantly affect torsional stiffness. For beams with uniform cross-sections along their length, the angle of twist under torsional load can be precisely calculated.
Polar Moment of Inertia and Torsional Resistance
The polar moment of inertia indicates a structural member’s ability to resist torsion. It is particularly important for beams subjected to twisting loads. This property can be calculated using the perpendicular axis theorem, which states that the polar moment of inertia is the sum of the moments of inertia about any two orthogonal axes passing through the axis of interest.
understanding the various properties of beams, including cross-sectional area, torsional constant, and moments of inertia, is essential for predicting and optimizing the behavior of structural elements under different loading conditions. These properties are fundamental in structural engineering, enabling the design of efficient, safe, and economical structures.
other Post
-
What is the RCC beam And what Types of RCC Beam?
-
Minimum And Maximum Percentage Of Steel In Column Beam Slab And Foundation
-
Calculate The Formwork For Columns Beam Girder And Slab