How to Find the Derivation of 0.42D Bent up Bar

In this article I will find the Derivation of 0.42d |what is the Crank Length of Bent up Bar |How to Find the Derivation of 0.42D Bent up Bar.

How to Find the Derivation of 0.42D Bent up Bar

Does anybody, know what is the length of a 45° bent-up bar?

This length is 0.42D or the length is 1.42D?

If you know this length is 0.42D Then is will explain how to come to the length of 0.42D

Now,

We calculate what is the 0.42D for bent up bar are

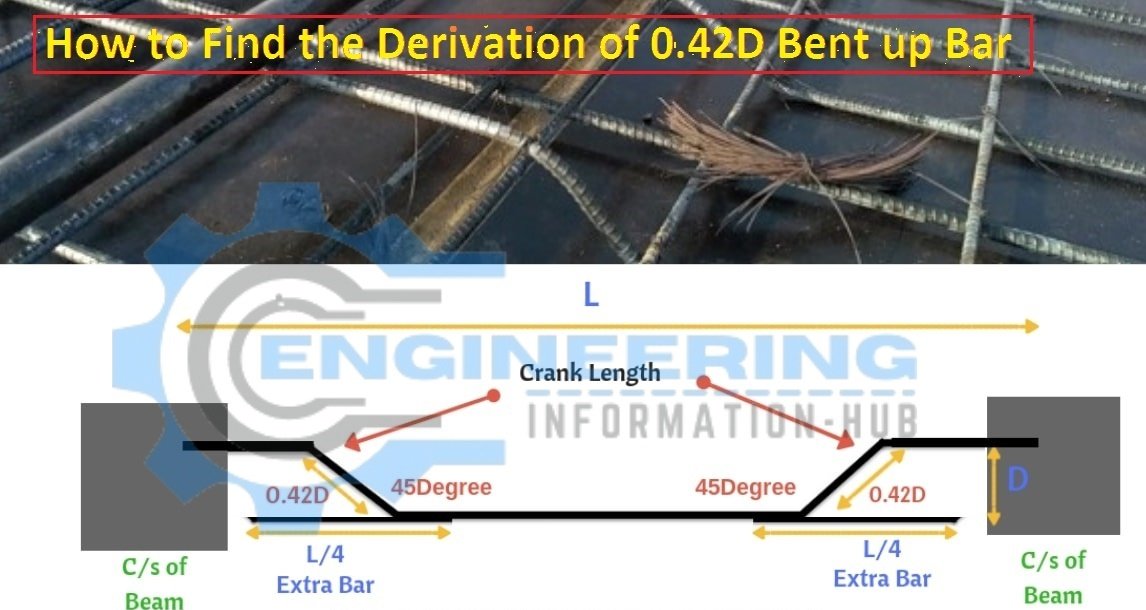
As you’ll observe within the diagram given below, the crank bar is bent at a 45° angle (by theory) in block reinforcement, & currently, we are going to derive the length of that bent-up half.

Let us draw a triangle in an exceedingly crank bar by naming the three corners as a, b, & c with sides ab, bc, & ca as shown below. Here, the bent-up part of the crank bar is called “side ac”.

Calculating the length of side ac:

Angle a = 180° – (angle b+ angle c )

∠a = 180° – ( 90° +45°)  = 45°

As it is symmetrical right angle triangle,

ab = bc = D

By Pythagoras theorem

ac2 = ab2+bc2

ac2 = D2+D2

ac2 = 2D2

ac =   √ 2D2

ac = 1.414D

Say ac = 1.42D

Derivation of 0.42D:

The cutting length formula for the crank bar, for the above-given drawing, is given by

The Cutting Length Formula for the Crank bar = Clearspan +2bends + 2x extra crank length) – (2× 90° bend + 4× 45°bends)

When we add the Clear Span within the Calculation, it means Already add side bc and side CB we need to take an Additional Remaining Length of the side ac by Deducting side bc from it.

Additional Crank Length = ac – bc

Additional Crank Length = 1.42D – 1D

Additional Crank Length = 0.42D

So, That’s What 0.42D Stands for Within the Cutting Length Formula.

Learn More

Bar Bending Schedule For R.C.C Beam

How To Estimate Per Meter Weight Of Reinforcements Steel Bar

The Alternate Technique for Confirmation

Known data:

side ab = D,

sin45°= 1/√2

sin45°=Perpendicular/ Hypotenuse

As per Above Triangle

sin45°=ab/ac

sin45°=D/ac

1/√2=D/ac

By Cross Multiplication,

ac ×1  = √2 D

ac = 1.414 D

We Can say Length of ac = 0.42D

Extra Crank Length = ac  bc  or  cb

Extra Crank Length = 1.42D – 1D

Extra Crank Length = 0.42D

So this is The Method to Find the Derivation of Crank Length of Bent up Bar = 0.42d

Learn More 

What Are The Causes Of Building Cracks

Bar Bending Schedule For The Staircase

Thanks for Reading Article Get more Information and share it with others.

JOIN US & LIKE MY OFFICIAL FACEBOOK PAGE 

THANKS